Deep Energy-Based NARX Models

Johannes Hendriks, Fredrik K. Gustafsson, Antônio Ribeiro, Adrian Wills, Thomas B. Schön

Abstract

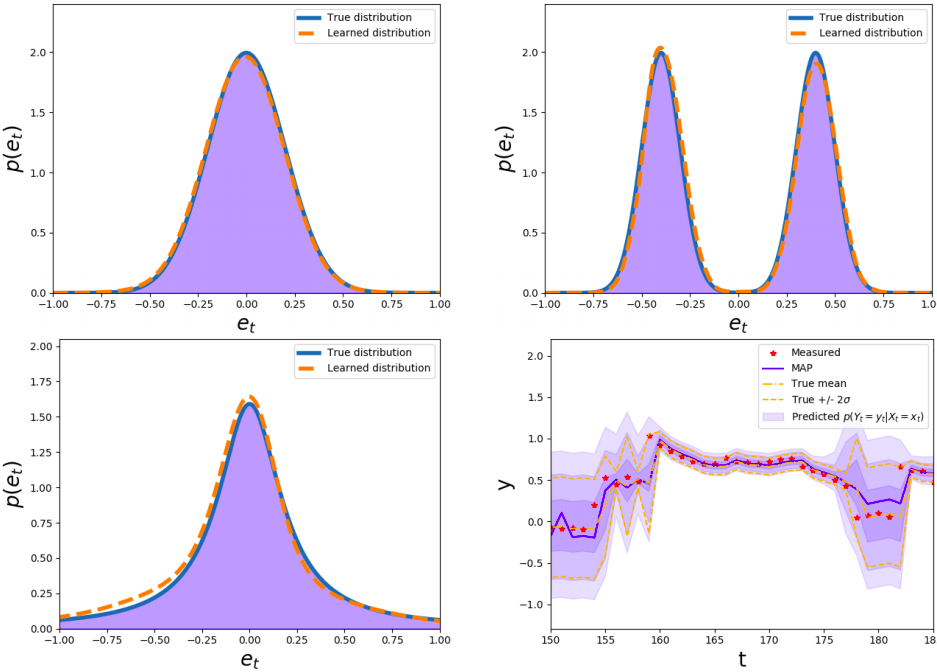
This paper is directed towards the problem of learning nonlinear ARX models based on system input–output data. In particular, our interest is in learning a conditional distribution of the current output based on a finite window of past inputs and outputs. To achieve this, we consider the use of so-called energy-based models, which have been developed in allied fields for learning unknown distributions based on data. This energy-based model relies on a general function to describe the distribution, and here we consider a deep neural network for this purpose. The primary benefit of this approach is that it is capable of learning both simple and highly complex noise models, which we demonstrate on simulated and experimental data.